En matemáticas, la sucesión de Fibonacci es la siguiente sucesión infinita de números naturales: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144...

La sucesión inicia con 1 y 1, y a partir de ahí, cada elemento es la suma de los dos anteriores.

A cada elemento de esta sucesión se le llama número de Fibonacci.

Esta sucesión fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci. Tiene numerosas aplicaciones en ciencias de la computación, matemáticas y teoría de juegos. También aparece en configuraciones biológicas, como por ejemplo en las ramas de los árboles, en la disposición de las hojas en el tallo, en la flora de la alcachofa y en el arreglo de un cono. Antes de que Fibonacci escribiera su trabajo, la sucesión de los números de Fibonacci había sido descubierta por matemáticos indios tales como Pingala (200 a.c.), Gopala (antes de 1135) y Hemachandra (c. 1150), quienes habían investigado los patrones rítmicos que se formaban con sílabas o notas de uno o dos pulsos.

La sucesión fue descrita por Fibonacci como la solución a un problema de la cría de conejos: "Cierto hombre tenía una pareja de conejos juntos en un lugar cerrado y desea saber cuántos son creados a partir de este par en un año cuando es su naturaleza parir otro par en un simple mes, y en el segundo mes los nacidos parir también".

Dicho de otra forma, sirve para conocer el número de conejos (parejas de conejos) que habrá en 12 meses, si estos se reproducen continuamente y cada pareja de conejos produce una nueva pareja de conejos (un macho y una hembra). Cada conejo se puede cruzar a la edad de un mes, siendo su periodo de gestación un mes. Siendo así, se tiene que:

El número áureo o de oro (también llamado número plateado, razón extrema y media, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) representado por la letra griega φ (fi) (en minúscula) o Φ (fi) (en mayúscula). Se trata de un número algebraico irracional (decimal infinito no periódico):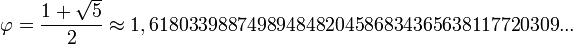 

 Posee muchas propiedades interesantes y fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción entre segmentos de rectas. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza. Puede hallarse en elementos geométricos, en las nervaduras de las hojas de algunos árboles, en el grosor de las ramas, en el caparazón de un caracol, en los flósculos de los girasoles, etc. Asimismo, se atribuye un carácter estético a los objetos cuyas medidas guardan la proporción áurea. Algunos incluso creen que posee una importancia mística. A lo largo de la historia, se ha atribuido su inclusión en el diseño de diversas obras de arquitectura y otras artes, aunque algunos de estos casos han sido cuestionados por los estudiosos de las matemáticas y el arte.

El número áureo es el valor numérico de la proporción que guardan entre sí dos segmentos de recta a y b que cumplen la siguiente relación:

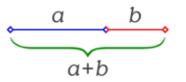
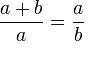
De aquí parte Lacan, sustituyendo en  a = 1 y b = a, es  ( 1+ a)/ 1= 1/a  o sea: 1 + a = 1 / a. Donde a = 0,618……, relación que guardan entre sí los números de la sucesión de Fibonacci. “Lo elegimos porque estábamos ante el problema preciso de saber cómo representar lo que se pierde al plantear arbitrariamente el 1 inaugural, reducido a su función de marca…Ocurre con él como con la perdida a la que apuntamos, que está en el horizonte de nuestro discurso, la que constituye el plus- de- gozar-- no es más que un efecto de la posición del rasgo unario” ( 129)

Esta relación la hace evidente el desarrollo de la serie decreciente de las a: puesto que a es menor que 1 y se expresa en la ecuación como potencia, se hará cada vez más pequeño a medida que se acerca a su límite: 1+ a. Como también se verifica esta relación en el desarrollo de la serie creciente que se inscribe en 1, los enteros van acrecentando su diferencia respecto  del número de las a: “de una extensión de los enteros del sujeto, tomado a nivel de la masa, siempre habrá una falta más grande  de unidades de a. No habrá a para todo el mundo”(131)

Lacan analizará la relación del 1 con el 1siguiente, en el que aparece la falta, como el sujeto dividido por la marca. La describe con el 1-1 que representa  la H de histérica remitiéndose a la identificación neurótica que refiere Freud como identificación al rasgo en Psicología de las masas y análisis del yo. De donde Lacan extrae el rasgo unario.

En un principio Lacan trata de articular la apuesta de  Pascal desde la teoría de los juegos, “la apuesta es coherente con la posición siguiente -- no podemos saber si Dios es ni lo que es”(133) , y se entabla sobre un discurso, la promesa de Dios de infinitas vidas infinitamente felices. Lo que se compromete es una postura “ese plus enigmático que nos hace a todos estar en el campo de cualquier discurso, a saber, el a”.(133)

Luego:“Infinidad de vidas infinitamente felices”,”….proliferación de enteros que sirven de apoyo a la proliferación de los objetos a?”(133), “Solo digamos que seguro que se trata de la serie creciente”.(134)

El a en relación al infinito de números enteros “se vuelve ineficiente…neutro”(134),- como hemos visto en el desarrollo de las series - por lo tanto cero, y  que sumado al infinito, se puede representar como cero. Esto de acuerdo a la combinatoria de la teoría de los juegos.

Se introduce el campo del discurso, representado por A: la promesa. Según la ley del juego, una jugada arriesgada debe considerarse perdida – con lo que verificamos la equivalencia de a = 0.

Si la promesa no es admisible – A no existe – la postura está perdida. Ya que nada de nosotros puede valer más allá de la muerte, tampoco el a; pero no es nada, sino que se pierde

Cuando introducimos al sujeto no ligado al simple establecimiento de esta matriz, sino de acuerdo al progreso engendrado a partir del psicoanálisis, Lacan dice: “…no es de ningún modo algo que podamos contentarnos de enmarcar con la conjunción de un número cualquiera de significantes….De toda conjunción significante resulta un efecto de caída…”(135). Se trata del sujeto divido, gracias a lo cual podemos escribir, construir una matriz.

Lacan hace el planteo desde Pascal, que dice:” están comprometidos”(137). El yo (je) está comprometido en la jugada que no se puede anular, ya que “Si es posible comprometer en el juego algo que sea a pérdida, es que la pérdida ya está allí.”(137). No se puede dejar de lado que todo enunciado del yo conlleva el deseo del Otro, representado en el contexto de Pascal por la Gracia:” un Hágase Tu Voluntad …( relación del sujeto con la demanda).., es lo que está en discusión cuando falta esta voluntad, precisamente por no ser la nuestra”(137) .”..y según la Gracia nos haya faltado o no, lo que se juega a nivel del Otro, a saber, de todo lo que nos precedió en ese discurso que determinó nuestra concepción misma, estamos obligados o no a correr para estancar el objeto a.”(139)                                                                                    

Según el Dios de Pascal:                                                                                               

Ahora los sujetos juegan y esto determina su conducta:

1º - Arriba izquierda, Dios existe ( lo sabe, lo cree) y apuesta a favor: renuncia a los placeres de la vida por infinitas vidas felices. Lacan describe a esta como la posición de sujeto purificado y señala la observación de Freud, de “ ..que a fin de cuentas, la creencia de los cristianos no los conduce a modificar su conducta de los que no lo son”.(138)

2º - Arriba derecha, Dios existe, pero apuesta en contra: pierde las infinitas vidas a cambio del a. Aquí Lacan ubica el infierno en que estamos y nos sucede todos los días, y que describe Pascal. Esta posición implica  interrogar la solidez del a hasta su límite mediante una medida indefinidamente repetida del corte de a.  La presencia de un menos infinito inclina a Lacan a tomarlo en su sentido aritmético: la serie de los enteros se redobla, es decir un semiifinito posible para esta casilla (2º), y que también equilibraría las oportunidades en la casilla 1º. Por tanto, Lacan recoge lo que se alude en el mito de Pascal, donde  “..la misericordia de Dios es mayor que su justicia”(139). Pues por el solo hecho de formar parte del dogma, aparta algunos elegidos, mientras que todos deberían estar en el infierno.

3º - Abajo derecha, Dios no existe y apuesta en contra: “conservan el a y duermen en paz.” (138). Esta aparente coherencia a Lacan  le sugiere la indiferencia del sujeto supuesto saber. En las casillas 1º y 3º: “..tienen ustedes gente que esta tan segura de su posición que , para ellos, no hay en absoluto apuesta. Siguen la corriente de lo que saben.”(138)

4º - Abajo izquierda, Dios no existe pero apuesta a favor: arriesga el a y lo pierde. Dado que forma parte de la naturaleza del a ser perdida y, que conservarla implica perder un menos infinito. Lacan destaca aquí aquellos que rechazan el a  sin importarles en absoluto la inmortalidad del alma:” sabios, plácidos padrazos, no solo padres.”(138)

Lacan ubica en esta casilla el análisis, o sea la buena norma. Pues allí se modula el plus-de-gozar fuera de toda promesa de retorno a la norma.

La norma se articula como la Ley, sobre la que se funda el Complejo de Edipo. Donde todo se ordena a partir del enunciado primero: está prohibido gozar de la madre. Esta formulación se confirma en Totem y tabú con el asesinato del padre, del que nos queda su función simbólica: el Nombre del Padre.