Hay una sucesión números, un patrón, una secuencia que aparece y reaparece en el mundo que conocemos. La podemos encontrar en la naturaleza, en la arquitectura, en la música, en la pintura, etc. Y le debemos su esclarecimiento a Leonardo de Pisa, más conocido como Fibonacci.

Nacido en 1175, Leonardo era hijo de un mercader italiano con intereses en el norte de África que lo inició en asuntos de contabilidad mercantil, despertando su interés por las matemáticas. Mientras recorrían sitios como Egipto, Sicilia, Grecia, le dejaba al cuidado de maestros árabes con quienes tuvo ocasión de conocer el sistema de numeración arábigo, los números con los que operamos en la actualidad. Hasta ese entonces, la Europa del medioevo continuaba utilizando los números de la antigua Roma, los números romanos. Ahora bien, ¿habéis intentado alguna vez hacer cuentas con números romanos?, ¿Y escribir un cifra con decimales?

Para el momento en que Leonardo y su padre regresan a Pisa, el niño trae consigo el conocimiento de la cultura árabe. A sus 37 años de edad escribe Liber Abaci, libro considerado un quiebre en la matemática occidental donde desarrolla la importancia del sistema de los números arábigos, y entre su contenido hay dos cosas que nos pueden interesar: el uso de la notación decimal y la incorporación del número cero, un número que pueda representar el valor de la nada. Sin embargo, la aceptación de este nuevo sistema numérico en aquella Europa Occidental tardó alrededor de tres siglos.

Fibonacci acompañaba sus explicaciones en Liber Abaci de una serie de enigmas y problemas, de entre los que se destaca uno en particular:

“¿Cuántas parejas de conejos tendremos a fin de año si, comenzando con una, produce cada mes una pareja que procrea otra pareja a los dos meses de vida?”

Entonces, podemos resolverlo pasando dato por dato a la siguiente tabla:

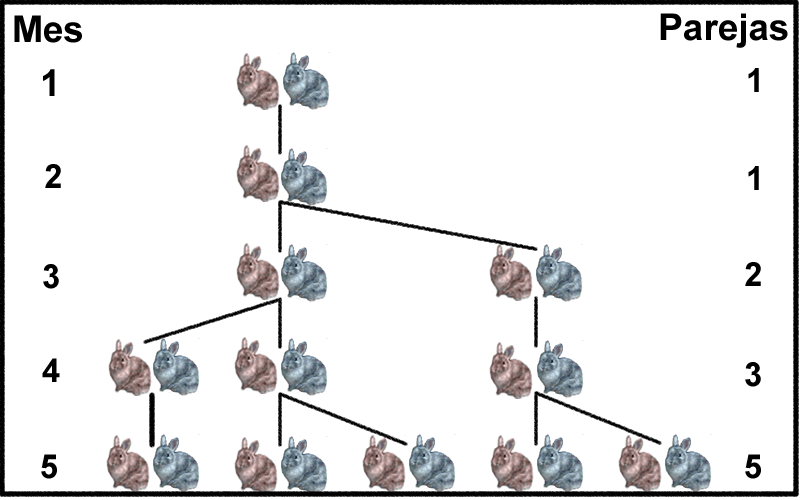
Si siguiéramos dibujando tendríamos 8 en el siguiente mes, luego 13, 21… y así hasta dibujar en el último mes del año 144 conejos.

Sin embargo, hay otra forma más sencilla de calcularlo. Esta serie de números que se aísla a la derecha y que comienza con [1,2,3,5,8,13,21…] es la llamada sucesión de Fibonacci y se caracteriza por el hecho de que cada término es igual a la suma de los dos precedentes.

1+1=2

1+2=3

2+3=5

3+5=8

Por lo que podríamos resolver el problema de los conejos haciendo esta misma operación hasta llegar al último mes. Verán que hemos llegado a igual resultado pero de una forma sumamente más sencilla.

Hay una segunda característica que define esta serie y es que en su interior contiene un número. Si tomamos dos números consecutivos de la serie y dividimos el mayor por el menor…

5/3= 1,666…

8/5= 1,6

13/8= 1,625

21/13= 1,615…

34/21=1,619…

… notaremos que a medida que avanzamos en la serie nos vamos a ir aproximando cada vez más a un número que empieza así:

1,618033987…

Digo “comienza” porque no sabemos muy bien cómo termina. Este número se conoce con el nombre de número de oro o razón áurea y se simboliza Φ (Phi). Es un número irracional, es decir, los decimales que contiene son infinitos y aperiódicos. Si quisiéramos llegar al momento en que más o menos se estabiliza la cifra deberíamos seguir repitiendo estas divisiones aproximadamente 11.003 veces. Entonces, hay una forma más sencilla de llegar a él, su fórmula es la siguiente:

1+√5

2

¿Cómo arribamos a ella?

Hagamos una representación gráfica aplicando las carácterísticas de la serie esta vez a segmentos. La línea C ha sido dividida en dos segmentos, A y B, tales que B es a A como A es a A+B, es decir, C:

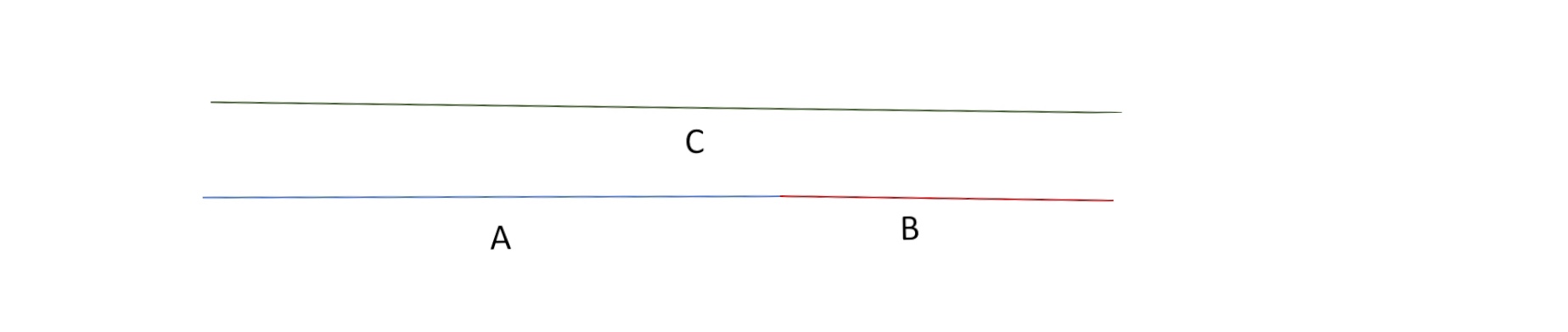
La relación entre segmentos son las llamadas proporciones y se escriben bajo la forma de fracciones. Entonces tenemos que:

A = A+B

B      A

A= A+ B

B   A   A

A= 1+ B

B        A

Además, sabemos por lo que vimos anteriormente en relación a la sucesión de Fibonacci, que la división del segmento mayor sobre el menor es igual a Φ.

Φ = 1+ B

            A

Φ = 1+ 1

            A/B

Φ = 1+ 1

            Φ

Me interesa que retengan en la memoria esta última ecuación, una de las representaciones posibles de Φ. Solo enseñaré, para que las conozcan, las derivaciones que le siguen para llegar al valor numérico de Φ.

Φ ² = Φ +( 1 . Φ )

                 Φ

Φ ²= Φ + 1

Φ ²- Φ -1 = 0

La solución positiva de esta ecuación, por equivalencias de polinomios, es

Φ = 1+√5

         2

Digo positiva porque la fórmula general tiene dos resultados posibles al ser en verdad + √5, pero por tratarse de un problema geométrico hemos de obtener un resultado positivo. Veréis que Lacan utilizando la variable negativa obtiene su inverso (0,618…), compartiendo las mismas características de Φ.

Si la hacéis en la calculadora comprobareis que hemos arribado al valor de Φ= 1,618…

Hay una curiosidad muy interesante de la que Lacan se servirá para abordar el capítulo 11 del Seminario 17 y es que los números irracionales, aquellos que se continúan de decimales infinitos y no periódicos, no pueden representarse en fracciones. ¿Y esto por qué?

Volvamos a esta fórmula que les pedí que recuerden.

Φ=1+1

        Φ

Ahora bien, al intentar sustituir el Φ bajo la barra por su valor tal como la igualdad nos enseña, acabaremos poniendo nuevamente 1+1 y así sucesivamente, de manera infinita. Φ

Φ =1+1

          1+1

              1+1

                   …

Podremos ver sencillamente que en su representación siempre queda un resto ineliminable, no hay fracción última que la sustituya para definirla. Es lo que se llama una fracción continua infinita.

Ahora bien, tenemos la sucesión de números de Fibonacci, la razón áurea, la fracción contínua infinita… ¿Cómo se relaciona todo esto con Lacan?

Lacan desarrolla con mayor detenimiento los usos de esta serie en el Seminario 16. Allí, intentará con el uso de las matemáticas lo que posteriormente describe como “una articulación más segura de lo que constituye el efecto de discurso”[1] . ¿A qué se refiere con el efecto de discurso? Lacan nos enseña cómo la incidencia del rasgo unario, de la marca significante sobre el cuerpo, tiene como efecto una pérdida ineliminable. Y “en este rasgo unario reside lo esencial del efecto de lo que, para nosotros, analistas, en el campo donde tratamos con el sujeto, se llama la repetición”[2].

Entonces, se pregunta Lacan, ¿cómo medir esta relación? ¿Cómo se articulan el rasgo unario y su efecto, es decir, a?

Si hablamos de la relación entre dos elementos en el mundo de la matemática ésta se escribe como una proporción. Entonces si buscamos la relación del 1 determinante con el efecto de la pérdida podemos escribirlo así:

1

a

Pero también sabemos que, en tanto la relación es una relación de pérdida, podemos decir que esta relación es igual a la conjunción (+) de 1 y su función de la pérdida, es decir a.

1= 1 + a

a

De esta misma proporción se deduce esta otra, que nos da el valor de a:

a=   1 

    1+a

a= 1 + 1

            a

Observémosla, ¿acaso no nos recuerda una fórmula que hemos descrito anteriormente?

a= 1 + 1             Φ = 1+ 1

            a                         Φ

Lacan homologa el valor de a al de Φ, aquel número irracional, que no se puede acabar de nombrar y que siempre se nos escapa saltando de un término a otro en la serie Fibonacci, intentando aproximarnos cada vez un poco más. En términos de Lacan, “ocurre con él [el número de oro] como con la pérdida a la que apuntamos, que está en el horizonte de nuestro discurso, la que constituye el plus-de-gozar —no es más que un efecto de la posición del rasgo unario.”[3]

La comparación del objeto con las propiedades del número de oro nos lleva, además, a problematizar la creencia en una complementariedad entre el sujeto y el objeto, la ilusión de completud. Lacan mismo nos lo advierte en el Seminario 16 al decir que “es grande la tentación de plantearse el sujeto del saber como sabiéndose a sí mismo”[4], cuando la diferencia entre el sujeto absoluto del goce y aquel engendrado por el rasgo unario es irremediable.

Ahora sí, entonces, habiendo llegado al final de la referencia tenemos los elementos necesarios para volver al capítulo 11 del Seminario 17 y, junto con Lacan, problematizar el cogito cartesiano y la dificultad de suponer un sujeto capaz de pensarse a sí mismo. No nos queda más que recordar la paradoja recursiva en la que entraría aquel sujeto que, como en una fracción continua infinita, formula: «Soy el que piensa “Luego yo soy”, el que piensa “Luego yo soy”, el que piensa “Luego yo soy”[5]… sucesivamente.