“Cuando ustedes tratan significantes matemáticos, que tienen otro estatus que nuestros pequeños significantes sexuados, y que penetran de otro modo en lo real, tal vez deberían intentar de todos modos destacar en su espíritu que hay al menos una cosa real, la única de la que estamos seguros: es el número. ¡Lo que llegamos a hacer con él! No se hizo poco. Para llegar a construir los números reales, es decir, justamente los que no lo son, el número debe ser algo real”¹. Es con esta introducción que intento aproximarme a lo real desde los números reales, a lo real en su espíritu desde el número. “El número nada tiene que ver con el lenguaje, y es más real que cualquier cosa”².

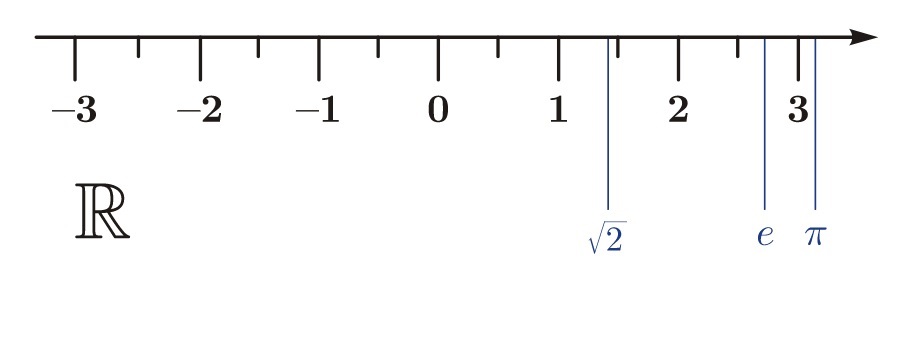
Entendemos los números reales como cualquier número que se encuentre en la recta real que incluye tanto a los números racionales como los irracionales en un dominio que va desde menos infinito a más infinito. En matemáticas este conjunto de los números reales es denotado con la letra mayúscula R, ¡valga la notación!. Los números reales se expresan con decimales que tienen una secuencia de dígitos a la derecha de la coma decimal, frecuentemente se añaden tres puntos suspensivos al final indicando que hay más dígitos decimales. Tomemos uno, el número real la raíz cuadrada de dos.

La raíz cuadrada de dos se define como el único número real positivo tal que multiplicado por sí mismo es igual a dos. Es decir, √2 x √2 = 2, un número que multiplicado por sí mismo alcance el resultado de dos. Podemos afirmar que a √2 lo bordean los números 1,41 y 1,42. Y podemos observar que al multiplicar 1,41 x 1,41 obtenemos 1,9881; mientras que 1,42 x 1,42  da como resultado 2,0164. En ambos casos nos encontramos con la imposibilidad del dos, algo falta, algo sobra. 

El valor numérico de √2 es aproximadamente 1,414… al que tal como aludimos se le añaden entonces tres puntos al final para indicar que hay más dígitos decimales. En busca de exactitud  le podemos agregar a 1,414… otro decimal 1,4142…, y otro 1,41421…. Sin embargo, aunque sigamos agregando decimales 1,414213…, nos encontramos con una captura fallida de decimales, algo se fuga. Podríamos continuar indefinidamente agregándole uno a uno los decimales después de la coma 1,414213562373095048801688724209698078569 … sin llegar nunca exactamente a él. Con cada nuevo decimal que no cesa de insistir, lo inaprensible hace escapar la exactitud, lo inaprensible “en cuanto a lo que no se tiene a su alcance”³. Lo que se escapa se hace visible. No se trata de “la reiteración computacional algorítmica”⁴ en tratar de aproximarse a lo real,  es la aproximación misma la que falla cada vez, es lo que hace real al número real. “La relación con el número es accesible para el lenguaje si este está fundado en la no relación sexual”⁵. Cita de Lacan que pareciera diseñada para este singular número real.

Lo inconmensurable existe.  Es en relación a lo inconmensurable que Lacan se referirá como a “las extravagancias del número”⁶. “Éstas comenzaron muy pronto”, nos dice, “ya en tiempos de Platón el número irracional presentaba dificultades y resultaba heredero de la perplejidad pitagórica por el carácter irracional de la diagonal del cuadrado, por el hecho de que jamás se terminará de calcularla. Esto es demostrable sobre una figura, y es justamente lo más acertado que había para revelarles desde esa época la existencia de lo que denomino la extravagancia numérica, quiero decir, de algo que surge del campo del Uno”⁷. En esta extravagancia del número es lo inconmensurable de la raíz cuadrada de dos la que nos muestra algo del orden de lo imposible. Un número real para la definición de un imposible.

Demostrable sobre una figura nos dice Lacan, observemos la diagonal del cuadrado o la hipotenusa del triángulo rectángulo. Un recurso para la representación de las raíces cuadradas es el uso de los triángulos rectángulos y circunferencias, explicándolo a partir del Teorema de Pitágoras. Si tomamos un triángulo rectángulo donde ambos catetos miden uno, tiene una hipotenusa  de carácter irracional, la raíz cuadrada de dos, todo un enigma si trabajamos con números enteros. Todo un enigma la combinación del número racional con el irracional en la figura misma de un triángulo rectángulo. Ahora bien, podríamos entonces representar la raíz cuadrada de dos en la recta numérica. Bastaría trazar sobre la recta real un triángulo rectángulo e isósceles de catetos unitarios y con un compás trazar un arco de circunferencia sobre la recta real de radio equivalente a la longitud de la hipotenusa del triángulo. La raíz cuadrada de dos se deja atrapar geométricamente, la podemos ubicar con exactitud sobre la recta real.

Estamos frente a una paradoja, lo inconmensurable de la raíz cuadrada de dos con sus infinitos decimales frente a la exactitud de la representación gráfica. ¿La paradoja como una forma de acceder a esa imposibilidad del número real? Nos dice Lacan, “el discurso analítico está hecho para recordarnos que el acceso a ese real del que hablo es lo simbólico. A dicho real sólo accedemos en y mediante ese imposible que sólo define lo simbólico”⁸. Pareciera que accedemos a la paradoja. “En matemáticas justamente a partir de lo imposible se engendra lo real”⁹.

“No zanjo la cuestión de si el número debe considerarse o no como algo real. Pero para no dejarlos en la ambigüedad la zanjo: el número forma parte de lo real. Pero es ese real privilegiado a propósito del cual el manejo de la verdad hace progresar la lógica”¹⁰. Para concluir entonces, y más allá del debate si el número debe considerarse o no como algo real, vemos al número zanjando ese imposible, vemos al número que nos acerca a lo inaprensible,  no lo podíamos obviar.